背景
工作后很少有时间进行理论知识的充电,抽出晚上的时间,再把吴恩达前辈的Deeplearning.ai课程过一遍,重在记录之前掌握不牢靠及容易忽视的知识点。
神经网络和深度学习
课程的第一讲,从经典的线性回归、逻辑回归、激活函数、损失函数、梯度下降几个方面,引出了神经网络知识,以下:
浅层神经网络
1、NN(neural networks)类似于多层逻辑回归网络,不断执行wx+b、激活、wa+b、激活….到loss function的计算
一张图代表逻辑回归和神经元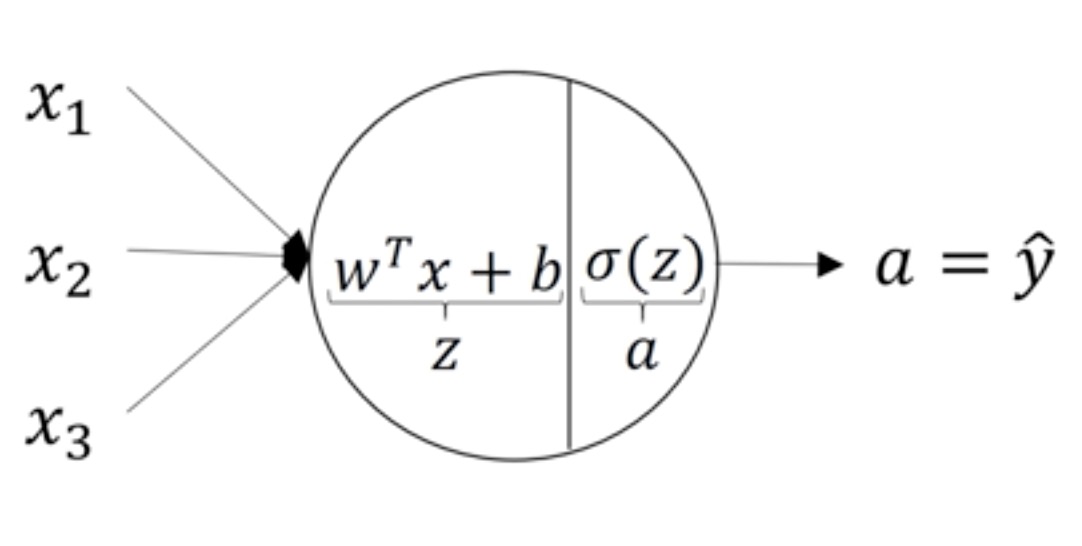
2、论文中一般说的两层神经网络,为input、hidden、output形式,默认input为0层。
3、对于一个样本:wx+b的循环转矩阵的快速运算,[4,3]乘[3,1]加[4,1] 等于4,1。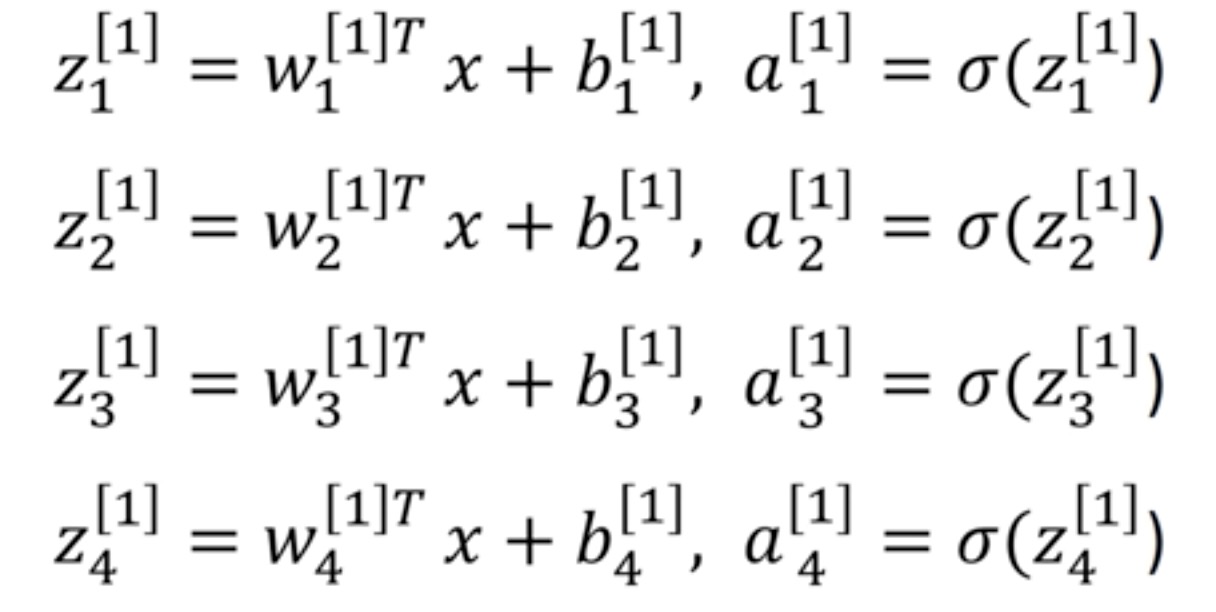
而对于batch个样本(此处假设有3个样本),即是把样本特征横向堆叠即可,即:[4,3]乘[3,3]加[4,3] 等于[4,3],如图示: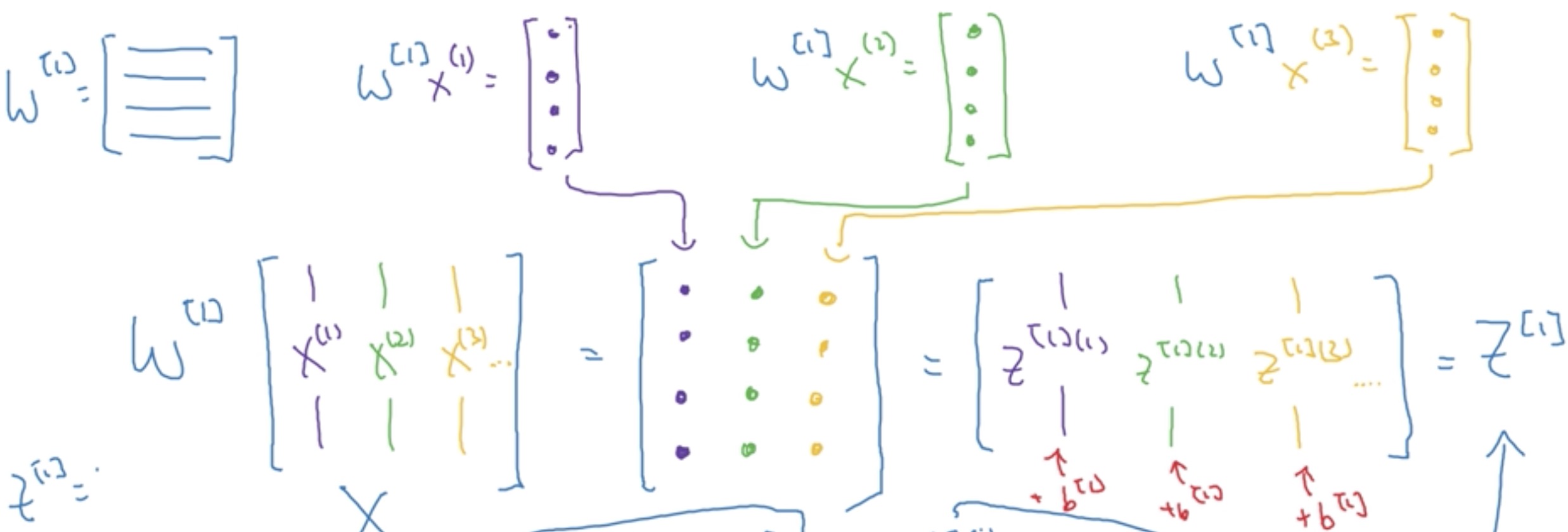
4、激活函数
sigmoid:最常用的二分类函数,表达式如下,导数为$g(z)(1-g(z))$,所以最大值为0.25
$$g(z)=\frac{1}{1+e^{-z}}$$
tanh:表达式如下,相当于将sigmoid函数平移,然后进行纵向拉伸(-1,1),除 了最后一层二分类使用sigmoid,中间的hidden layer极力推荐tanh取代它。但这两个函数在Z很大或者很小时,都会发生梯度消失,导数趋近于0。tanh的导数为$(1-g(z)^{2})$
$$g(z)=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}$$
Relu:表达式为:$a = max(0,z)$,相对来说不容易梯度消失,Z>0时,导数为1,Z<0时,导数为0。Z=0时不可导,我们指定它为0或1就好了(实际Z=0的概率非常低)。三者中目前较常用的函数是Relu,对于拥有大量节点的神经网络来说,总会有很多Z>0的神经元,梯度下降速度还是比较可观的。
leaker Relu:表达式为:$a = max(0.01\ast z,z)$,此处的0.01是个参数,你可以改成其它值进行尝试,说到底就是梯度下降速度的问题(太大了可能扯着蛋…)
5、神经网络权重(w)不能初始化为全0,因为这样导致每个神经元对输出的贡献是一样的,所以反向传播后神经元修正也一样。换句话说每个隐藏单元都在计算一样的函数,没有什么意义。python:$ w = np.random.randn((2,2))0.01,如前所示,浅层神经网络用接近0的一个高斯分布随机值初始化。深层NN吴恩达老师卖了个关子,且听下次分解吧
改善深层神经网络
主要解决神经网络超参数优化原因及方法
正则化缓解过拟合
L2正则化(有时也称weight decay):$J_{new} = J + \frac{\lambda}{2m}\left | w \right |^{2}$,其中$\left | w\right |^{2} = \sum_{j=1}^{n}w_{j}^{2} = w^{T}w$。或者如下公式(m:样本数量,n:权重w数量),可以看到lambda足够大时,会使得权重矩阵w很小,大致想象,再深的网络都可以化为逻辑回归的样式。
$$min_{\theta } \frac{1}{2m} \sum_{i=1}^{m}(h_{\theta }(x^{i})-y^{i})^{2}+\lambda \sum_{j=1}^{n}\theta_{j}^{2}$$
换种较理性的方式来解说是:假如激活函数采用tanh,lambda越大,w越小,$g(z)=wx+b$越小,激活函数此时位于斜率$k=1$的线性段(相对来说比较线性的区间),线性激活函数是拟合不出复杂的边界的。
Dropout正则化
反向随机失活推导
其它缓解过拟合的方法
数据扩充(左右对称、随机裁剪放大、旋转一定角度、扭曲),early stoping