背景
以一个单隐层神经网络简要说明反向传播算法的推导过程，需要注意的一点就是同步更新网络参数，即：在一次方向传播算法中，需要先求所有参数的偏导数，再同时更新参数。而不能以反向传播中较深层次已经更新的参数，带入偏导式子再更新浅层参数。（直观的理解就是多维度上的同步下降）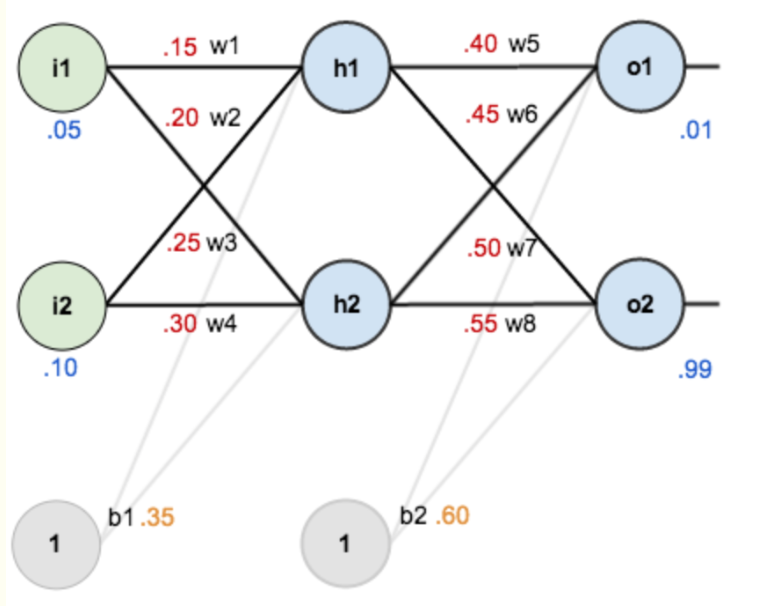
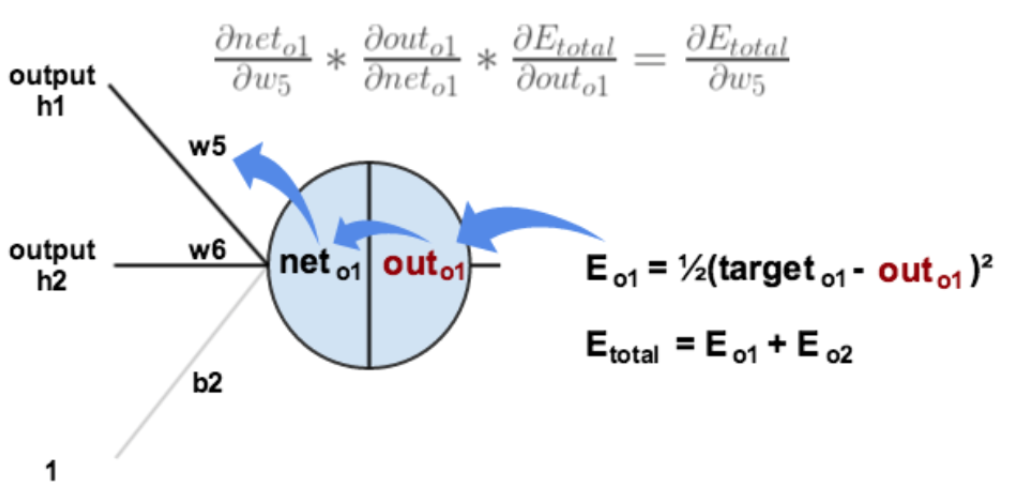某个神经元相对于总误差的误差率：是上一层各个神经元的误差率，乘，对应到该层某个神经元的权值，再加和。之后对该神经元激活函数求导$$\delta_{h1}=\sum_{i=0}^{n}\delta_{i}w_{i}\ast out_{h1}(1-out_{h1})$$推导过程中也可以看到梯度消失的原因，每经过一个神经元，都会有sigmoid函数导数产生，用于连乘积，而该值最大值为y*(1-y)=0.25
