概念先行
正态分布(Normal distribution),又名高斯分布(Gaussian distribution),呈钟型,两头低,中间高。数学定义:随机变量X服从一个数学期望为μ、方差为σ^2的正态分布,记为N(μ,σ^2)。其中期望值μ决定了其集中趋势位置;标准差σ决定了分布的幅度,σ越大,曲线越扁平,反之σ越小,曲线越瘦高。标准正态分布:当μ = 0,σ = 1时是标准正态分布。方差:sum(x-u)^2/N
一个简单的神经网络
对于z = np.sum(x*w),假如w为一个1000维的向量,服从均值为0、方差为1的正态分布,输入层x一共1000个神经元,且全为1。所以z服从的是一个均值近似为0、方差为1000的正态分布:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25# -*- coding:utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
def run():
# z的个数
t = 20000
z_lst = np.empty(t)
x = np.ones(1000)
b = 0
for i in xrange(t):
w = np.random.randn(1000) #从标准正态分布中返回一个或多个样本值
# w = np.random.rand(1000) # 返回[0,1)之间的随机样本
#plt.hist(w, bins=50, normed=1)
#plt.show()
z = np.sum(x * w) + b
z_lst[i] = z
print 'z 均值:', np.mean(z_lst)
print 'z 方差:', np.var(z_lst)
plt.hist(z_lst, bins=50, normed=1) # hist直方图绘制函数,bins:直方图的柱数,默认为10,normed:是否进行归一化
plt.show()
if __name__ == "__main__":
run()
从图中看出:z有非常大的概率是一个远小于-1或者远大于1的数,通过激活函数(比如sigmoid)后所得到的输出非常接近0或者1。这样一来对权重的微小调整,基本不会使得隐藏层z的神经元激活值发生变化。BP时,权重更新就会非常慢。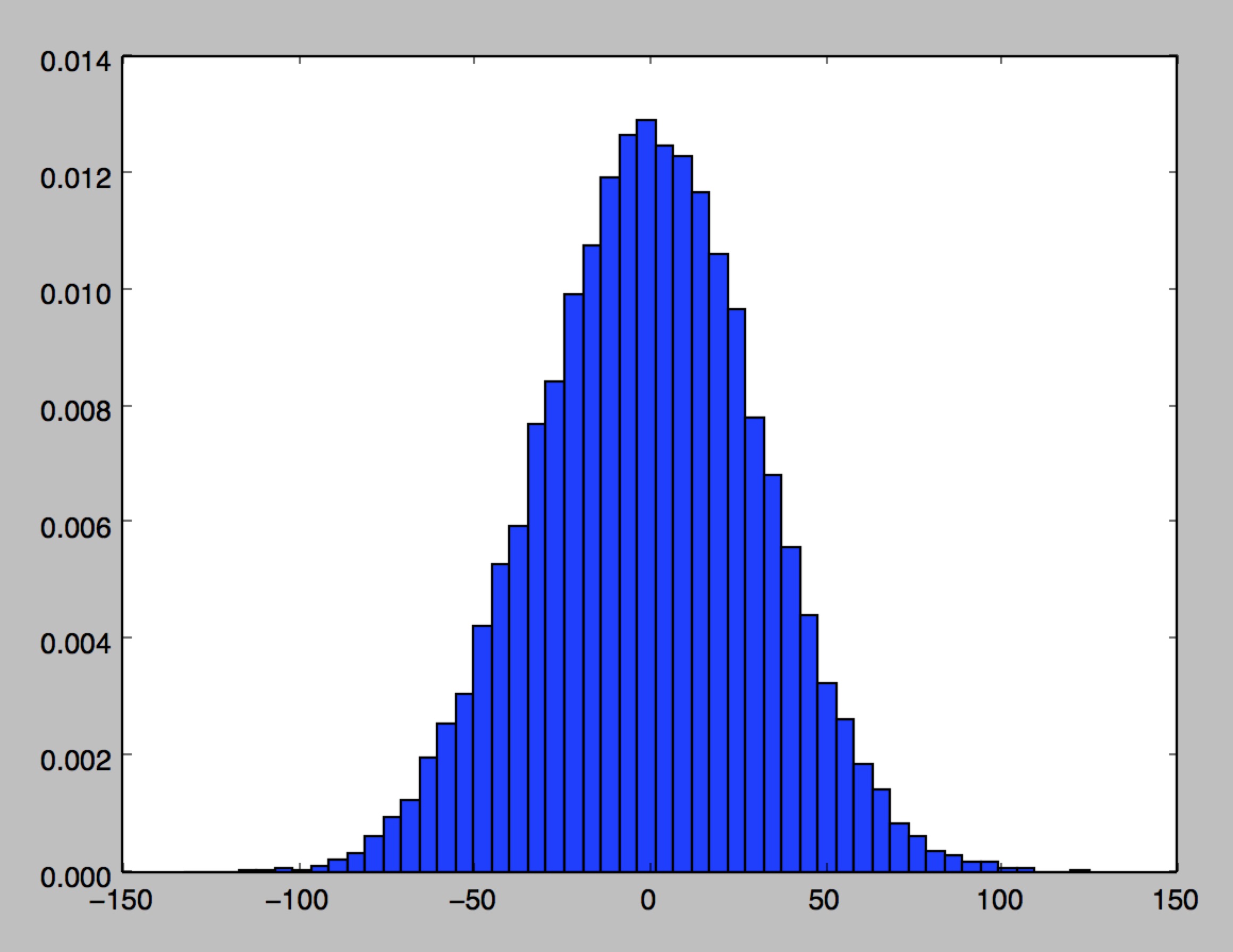
Target:那么我们的目标就是通过改变权重矩阵w的分布,使|z|尽量接近于0。经过激活函数后神经元的变化便会比较敏感。
怎样进行权重初始化
根据上述方差的计算公式:sum(x-u)^2/N ,只要x缩小sqrt(m)倍,总的方差便缩小m倍。对上述代码进行改进:1
2
3
4
5
6
7w = np.random.randn(1000)/np.sqrt(1000)
# 保持与z分布(1)图像横坐标刻度不变,使得结果更加直观
plt.xlim([-150, 150])
plt.hist(z_lst, bins=50)
plt.show()
#z 均值: 0.013468729222
#z 方差: 1.00195898464
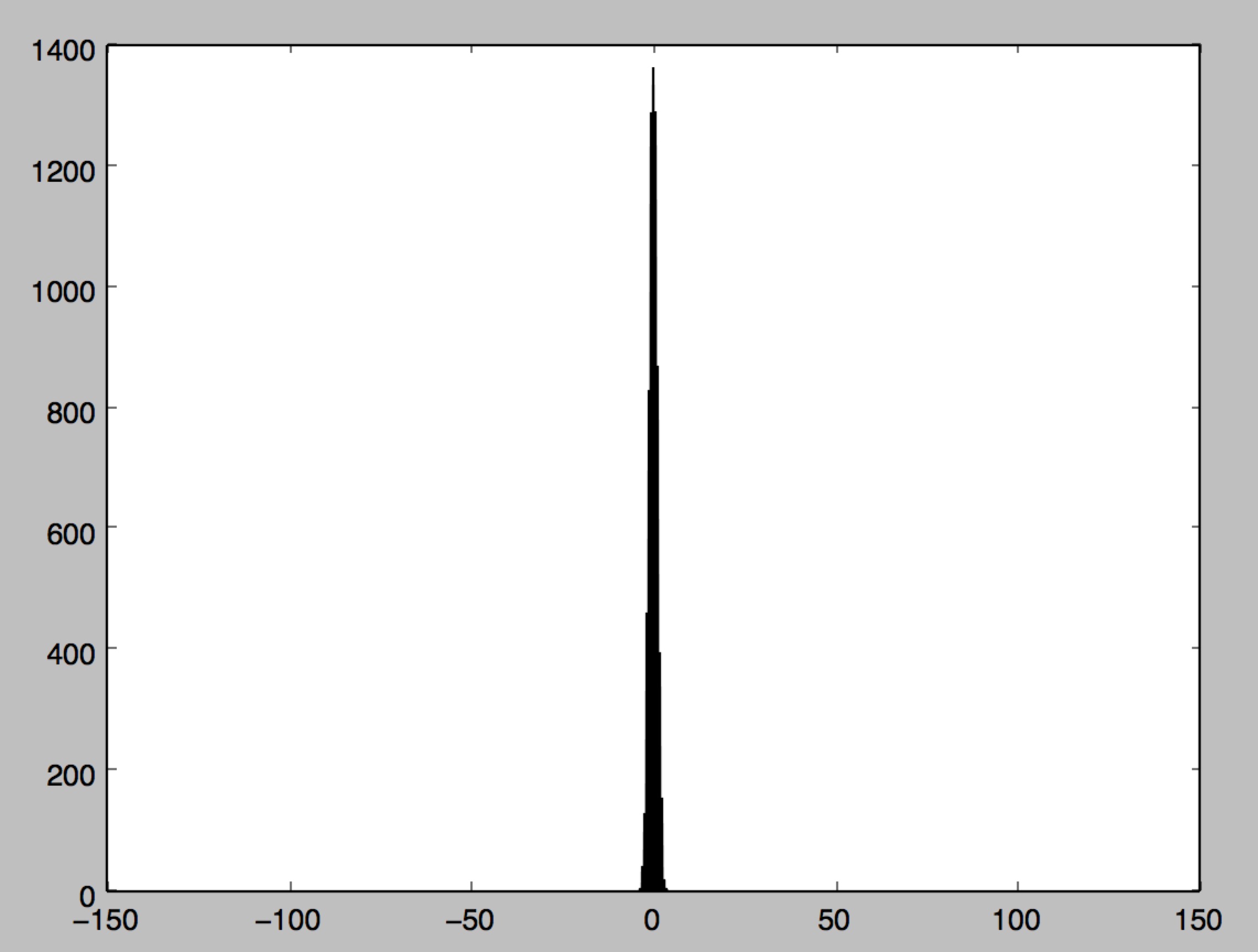
由上图可以看出,隐藏层神经元z的分布是一个比较接近于0的数,使得神经元的变化比较敏感,让BP过程能够正常进行下去。